
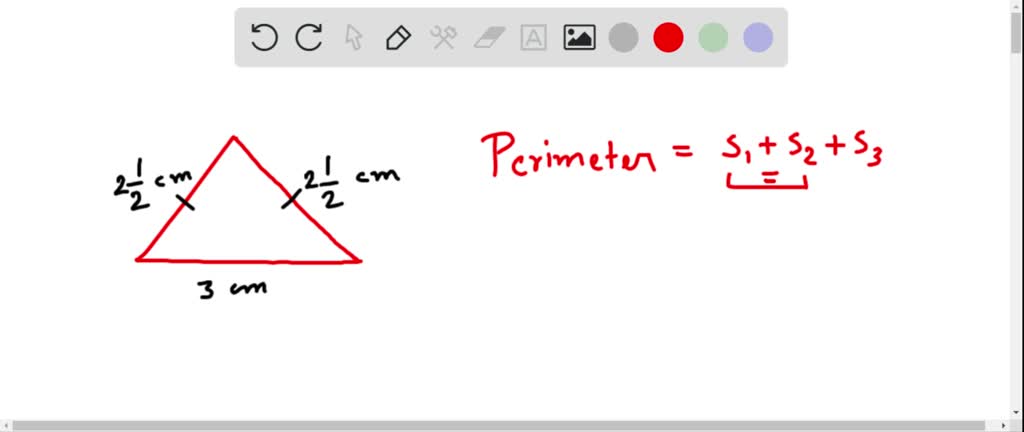
What is an Isosceles Triangle?Ī polygon with at least two sides of equal length, angles, three vertices, and three edges is an isosceles triangle. Right Angle TriangleĪ triangle with only one interior angle of 900 is known as a right-angle triangle. Obtuse Angle TriangleĪ triangle with one interior angle of more than 900 is an obtuse angle triangle. Acute Angle TriangleĪ triangle with all of its interior angles less than 900 is known as an acute angle triangle. Scalene TriangleĪll three sides are unequal in length. They have three vertices, three sides, three angles and are classified into three types according to the lengths of their sides, such as:Īll three sides are equal in length. Types of TrianglesĪ two-dimensional geometric shape made up of three-line segments connected at their endpoints or vertices is known as a triangle. Before discussing the isosceles triangles' properties, let us have a quick overview of the classification and angles of triangles. Interestingly, all types of triangles, such as the isosceles triangle or scalene, form out of straight-line segments with some angles and side length. Therefore, understanding the basic concepts, properties, type, angles, and every other detail is considered important by all the private math tutors and teachers around the globe. QU is an angle bisector of Δ QRS because it bisects ∠ RQS.Triangles are one of the most used and one of the first shapes studied in geometry. SP is a median to base QR because P is the midpoint of QR. RT is an altitude to base QS because RT ⊥ QS. In Figure, the altitude drawn from the vertex angle of an isosceles triangle can be proven to be a median as well as an angle bisector.įigure 9 The altitude drawn from the vertex angle of an isosceles triangle.Įxample 1: Based on the markings in Figure 10, name an altitude of Δ QRS, name a median of Δ QRS, and name an angle bisector of Δ QRS.įigure 10 Finding an altitude, a median, and an angle bisector. In certain triangles, though, they can be the same segments. In general, altitudes, medians, and angle bisectors are different segments. In every triangle, the three angle bisectors meet in one point inside the triangle (Figure 8).įigure 8 The three angle bisectors meet in a single point inside the triangle. In Figure, is an angle bisector in Δ ABC. Every triangle has three angle bisectors. In every triangle, the three medians meet in one point inside the triangle (Figure 6).įigure 6 The three medians meet in a single point inside the triangle.Īn angle bisector in a triangle is a segment drawn from a vertex that bisects (cuts in half) that vertex angle. Which may or may not be inside the triangle.Ī median in a triangle is the line segment drawn from a vertex to the midpoint of its opposite side. It is interesting to note that in any triangle, the three lines containing the altitudes meet in one point (Figure 4).įigure 4 The three lines containing the altitudes intersect in a single point, įigure 3 An altitude for an obtuse triangle. In Figure 3, AM is the altitude to base BC. įigure 2 In a right triangle, each leg can serve as an altitude. In Figure 2, AC is an altitude to base BC, and BC is an altitude to base AC. Every altitude is the perpendicular segment from a vertex to its opposite side (or the extension of the opposite side) (Figure 1).įigure 1 Three bases and three altitudes for the same triangle.Īltitudes can sometimes coincide with a side of the triangle or can sometimes meet an extended base outside the triangle. Now isn't that kind of special?Įvery triangle has three bases (any of its sides) and three altitudes (heights). Just as there are special names for special types of triangles, so there are special names for special line segments within triangles. Summary of Coordinate Geometry Formulas.Slopes: Parallel and Perpendicular Lines.Similar Triangles: Perimeters and Areas.Proportional Parts of Similar Triangles.Formulas: Perimeter, Circumference, Area.Proving that Figures Are Parallelograms.
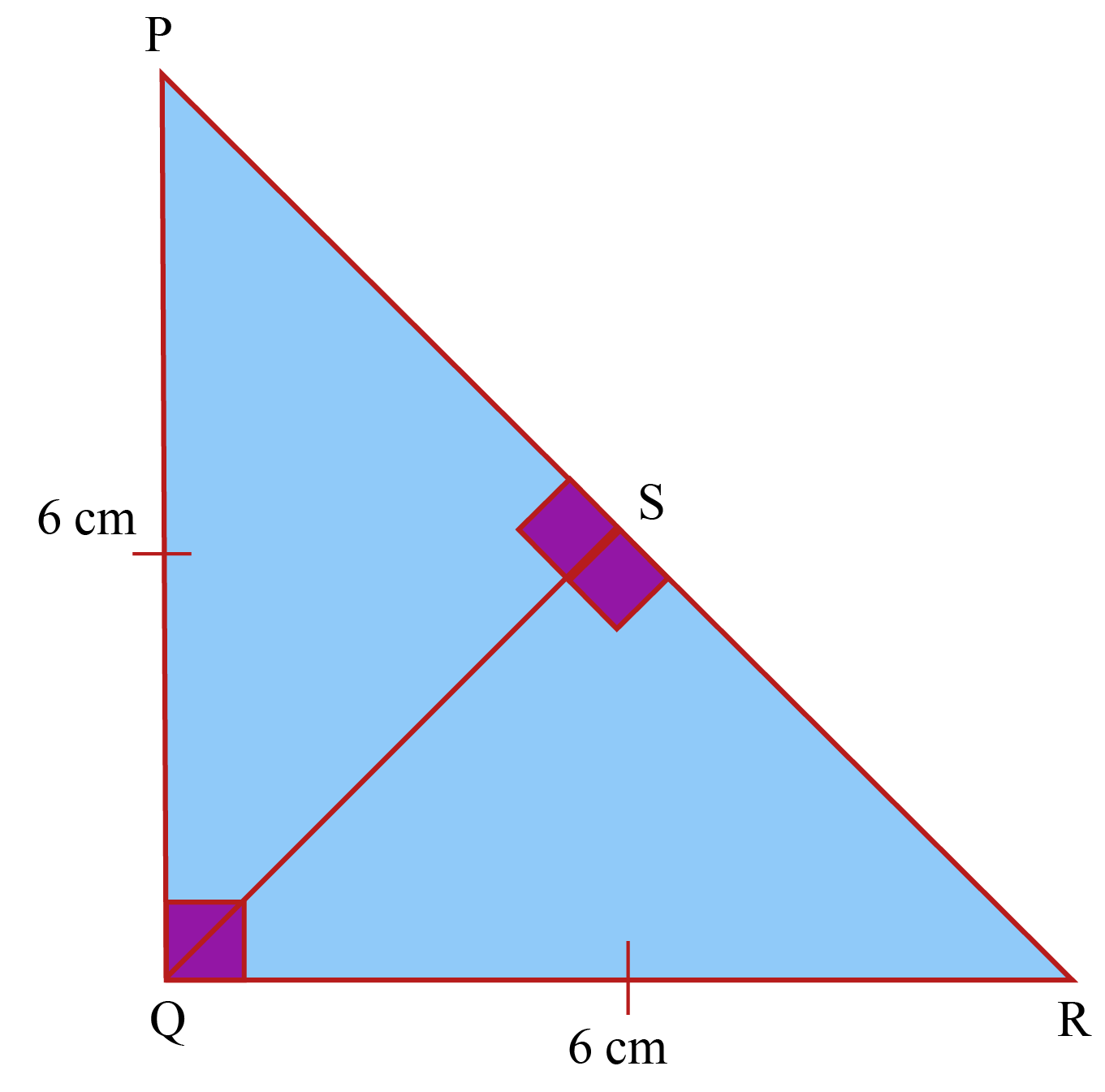

Triangle Inequalities: Sides and Angles.Special Features of Isosceles Triangles.Classifying Triangles by Sides or Angles.Lines: Intersecting, Perpendicular, Parallel.


 0 kommentar(er)
0 kommentar(er)
